Lecture 3: Review of Statistics
Zheng Tian
Created: 2017-02-26 Sun 21:29
Estimation of the Population Mean
The goal of estimation
- Suppose we draw \(n\) random samples, \(Y_1, \ldots, Y_n\), and \(Y_i \sim IID(\mu_Y, \sigma^2_Y)\) for \(i=1, \ldots, n\).
- The goal is to estimate \(\mu_Y\) given these \(n\) samples. A natural way is to compute the sample average, \(\overline{Y}\).
Estimators
- An estimator is a function of a sample of data to be drawn randomly from a population.
- An estimate is the numerical value of the estimator when it is actually computed using data from a specific sample.
- An estimator is a random variable because of randomness in selecting the sample, while an estimate is a nonrandom realization of the estimator.
Estimators of \(\mu_Y\)
- \(\overline{Y} = (1/n)\sum_{i=1}^n Y_i\) is an estimator of \(\mu_Y\).
- \(Y_1\), the first observation, can also be used as an estimator because it is indeed a function of sample data.
- As such, we can have many different estimators of \(\mu_Y\). How can we judge which estimator is better than another?
Unbiasedness
Definition of unbiased estimators
Let \(\hat{\mu}_Y\) be an estimator of \(\mu_Y\). The estimator \(\hat{\mu}_Y\) is said to be unbiased if
\[\mathrm{E}(\hat{\mu}_Y) = \mu_Y\]
where \(\mathrm{E}(\hat{\mu}_Y)\) is the expectation of the sampling distribution of \(\hat{\mu}_Y\).
Are \(\overline{Y}\) and \(Y_1\) unbiased?
\(\overline{Y}\) is an unbiased estimator of \(\mu_Y\).
In Lecture 2, we have already shown that \(\mathrm{E}(\overline{Y}) = \mu_Y\) when \(Y_i \sim IID(\mu_Y, \sigma^2_Y)\) for \(i=1, \ldots, n\).
\(Y_1\) is also an unbiased estimator.
\(\mathrm{E}(Y_1) = \mu_Y\) when \(Y_1\) is drawn from \(IID(\mu_Y, \sigma^2_Y)\).
Consistency
Definition of consistent estimators
\(\hat \mu_Y\) is a consistent estimator of \(\mu_Y\) if \(\hat{\mu}_Y\) is convergent in probability to \(\mu_Y\).
That is, \(\hat{\mu}_Y\) is consistent if \[\hat{\mu}_Y \xrightarrow{\text{ p }} \mu_Y \text{ as } n \rightarrow \infty\]
Are \(\overline{Y}\) and \(Y_1\) consistent?
\(\overline{Y}\) is a consistent estimator of \(\mu_Y\).
The law of large number ensures that \(\overline{Y} \xrightarrow{\text{ p }} \mu_Y\) is true when \(Y_i \sim IID(\mu_Y, \sigma^2_Y)\) for \(i=1, \ldots, n\), and \(\sigma^2_Y < \infty\).
- However, we cannot assess the consistency for \(Y_1\) because it cannot be written as the form of an average.
Variance and efficiency
Definition of efficient estimators
- When both \(\tilde{\mu}_Y\) and \(\hat{\mu}_Y\) are two unbiased estimators of \(\mu_Y\), we choose the estimator with the tightest sampling distribution, which means the smallest variance.
- \(\hat{\mu}_Y\) is said to be more efficient than \(\tilde{\mu}_Y\) if \[\mathrm{Var}(\hat{\mu}_Y) < \mathrm{Var}(\tilde{\mu}_Y)\]
- In words, \(\hat{\mu}_Y\) is more efficient than \(\tilde{\mu}_Y\) because \(\hat{\mu}_Y\) uses the information in the data more efficiently than does \(\tilde{\mu}_Y\).
\(\overline{Y}\) is more efficient than \(Y_1\)?
- In Lecture 2, we compute the variance of \(\overline{Y}\) to be \(\sigma^2_Y / n\) when \(Y_i \sim IID(\mu_Y, \sigma^2_Y)\).
- The variance of \(Y_1\) is \(\sigma^2_Y\).
- When \(n > 1\), \(\overline{Y}\) is more efficient than \(Y_1\).
\(\overline{Y}\) is the best linear unbiased estimator (BLUE)
BLUE
- \(\overline{Y}\) happens to be the Best Linear Unbiased Estimator (BLUE).
- It means that among all linear unbiased estimator, \(\overline{Y}\) has the smallest variance.
Linear estimators and \(\overline{Y}\) is BLUE
- A linear estimator of \(\mu_Y\) is a weighted average of \(Y_1, \ldots, Y_n\), written as \[ \tilde{\mu}_Y = \frac{1}{n} \sum_{i=1}^n \alpha_i Y_i \] where \(\alpha_1, \ldots, \alpha_n\) are nonrandom constants.
- If \(\tilde{\mu}_Y\) is another unbiased estimator of \(\mu_Y\), then we always have \(\mathrm{Var}(\overline{Y}) \leq \mathrm{Var}(\tilde{\mu}_Y)\), and the equality holds only if \(\tilde{\mu}_Y = \overline{Y}\). It means that \(\overline{Y}\) is BLUE.
\(\overline{Y}\) is the least squares estimator of \(\mu_Y\)
A linear model for the population mean
- Consider the following model \[ Y_i = \alpha + u_i \text{ for } i = 1, 2, \ldots, n \] where \(\alpha\) is a nonrandom intercept to be estimated.
- \(u_i\) is the error term, which is a random variable with \(\mathrm{E}(u_i) = 0\). Thus, we have \(E(Y_i) = \alpha = \mu_Y\).
- \(u_i\) can be seen as the error of predicting \(Y_i\) with \(\alpha\) for each \(i\), and we use \[\sum_{i=1}^n (Y_i - \alpha)^2\] to measure the total prediction errors.
- A natural choice of an estimator of \(\alpha\) is the one that minimizes this sum of squared errors.
The least squares estimator
- The least squares estimator of \(\mu_Y\) (or \(\alpha\)) is obtained by solving the following problem \[ \operatorname*{min}_a\: \sum_{i=1}^n (Y_i - a)^2 \]
- The solution of this minimization problem is just \(a = \overline{Y}\).
The proof for \(\overline{Y}\) is the least square estimator
The first order condition for the minimization problem is
\begin{equation*} \frac{d}{da}\sum_{i=1}^n (Y_i - a)^2 = -2\sum_{i=1}^n(Y_i - a) = -2\sum_{i=1}^n Y_i+ 2n a = 0 \end{equation*}- Solving the equation for \(a\), we get \(a = 1/n\sum_{i=1}^n Y_i = \overline{Y}\).
Hypothesis Tests Concerning the Population Mean
The null hypothesis
- Hypothesis testing is thus to make a provisional decision based on the evidence at hand on.
- The hypothesis of the population mean, \(\mathrm{E}(Y)\), taking on a specific value, \(\mu_{Y,0}\). So the null hypothesis, denoted as \(H_0\), is \[ H_0: E(Y) = \mu_{Y,0} \]
The alternative hypothesis
- The alternative hypothesis, denoted as \(H_1\)
- The two-sided alternative: \(H_1: E(Y) \neq \mu_{Y,0}\)
- The one-sided alternative: \(H_1: E(Y) > \mu_{Y,0}\)
The language
One thing should be kept in mind is that we usually do not say "accept the null hypothesis" when the hypothesis test is in favor of the null, but say "fail to reject the null".
Test statistics
The z-statistic when \(\sigma_Y\) is known
- We know that when \(Y_i \sim IID(\mu_Y, \sigma^2_Y)\) for \(i=1, \ldots, n\), \(E(\overline{Y}) = \mu_Y\) and \(\mathrm{Var}(\overline{Y}) = \sigma^2_{\overline{Y}} = \sigma^2_Y / n\).
- In the null hypothesis, we specify \(\mu_Y = \mu_{Y,0}\).
So given that \(\sigma_Y\) is known, the z-statistic is computed as
\[ z = \frac{\overline{Y} - \mu_{Y,0}}{\sigma_{\overline{Y}}} = \frac{\overline{Y} - \mu_{Y,0}}{\sigma_Y/\sqrt{n}} \]
- As \(n \rightarrow \infty\), by the central limit theorem, we know \(z \xrightarrow{\text{ d }} N(0, 1)\).
The t-statistic when \(\sigma_Y\) is unknown
- Of course, \(\sigma_Y\) is the standard deviation of the population variance that is usually unknown. So we need to replace \(\sigma_Y\) with its estimator.
The sample variance and standard deviation
The sample variance \(s^2_Y\) is is an estimator of the population variance \(\sigma^2_Y\), which is computed as
\[ s^2_Y = \frac{1}{n-1}\sum^n_{i=1} (Y_i - \overline{Y})^2 \]
- The sample standard deviation, \(s_Y\), is the square root of \(s^2_Y\)
The sample variance, \(s^2_Y\), is a consistent estimator of the population variance, that is, as
\[ n \rightarrow \infty, s^2_Y \xrightarrow{\text{ p }} \sigma^2_Y\]
The standard error of \(\overline{Y}\)
The standard error of \(\overline{Y}\), denoted as \(SE(\overline{Y})\) or \(\hat{\sigma}_{\overline{Y}}\), is an estimator of the standard deviation of \(\overline{Y}\), \(\sigma_{\overline{Y}}=\sigma_Y/\sqrt{n}\), with \(s_Y\) replacing \(\sigma_Y\).
\[ SE(\overline{Y}) = \hat{\sigma}_{\overline{Y}} = \frac{s_Y}{\sqrt{n}} \]
The t-statistic
- When \(\sigma_Y\) is unknown, by replacing \(\sigma_Y\) with \(s_Y\), we have the t statistic
\[ t = \frac{\overline{Y} - \mu_{Y,0}}{SE(\overline{Y})} = \frac{\overline{Y} - \mu_{Y,0}}{s_Y/\sqrt{n}} \]
- The asymptotic distribution of the t statistic is \(N(0, 1)\) because \(s_Y\) is a consistent estimator of \(\sigma_Y\).
- When \(Y_i\) for \(i=1, \ldots, n\) are i.i.d. from \(N(\mu_Y, \sigma_Y^{2})\), we can show that the exact distribution for the t statistic is the student t distribution with \((n-1)\) degrees of freedom. That is \[ t \sim t(n-1) \]
Hypothesis testing with a pre-specified significance level
Type I and type II errors
- A statistical hypothesis test can make two types of mistakes:
- Type I error. The null hypothesis is rejected when in fact it is true.
- Type II error. The null hypothesis is not rejected when in fact it is false.
The significance level and the critical value
- The significance level is the pre-specified probability of type I error. Usually, we set the significance level to be \(\alpha = 0.05, 0.10, \text{ or } 0.01\).
- The critical value, denoted as \(c_{\alpha}\), is the value of the test statistic for which the test rejects the null hypothesis at the given significance level. The \(N(0, 1)\) critical value for a two-sided test with a 5% significance level is 1.96.
The rejection rule and rejection region
- The rejection rule. For a two-sided test, we reject the null hypothesis when \(|z^{act}| > c_{\alpha}\).
- The rejection region is the set of values of the test statistic for which the test rejects the null, and the acceptance region is the vice.
The rejection region illustrated
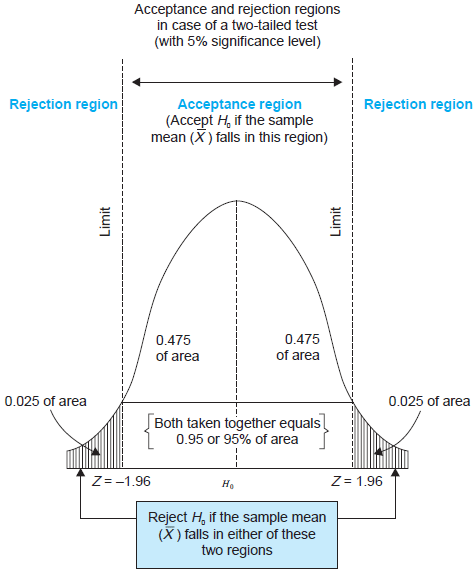
Figure 1: An illustration of a two-sided test
The power and the size of the test
- The size of the test is the probability that the test actually incorrectly rejects the null hypothesis when it is true. That is, the size of the test is just the significance level.
The power of the test is the probability that the test correctly rejects the null when the alternative is true. That is,
\[\text{power} = 1 - \mathrm{Pr}(\text{type II error})\]
The p-value
- The p-value, also called the significance probability, is the probability of drawing a statistic at least as adverse to the null hypothesis as the one you actually computed in your sample, assuming the null hypothesis is correct.
The p-value provides more information than the significance level.
In fact, the p-value is also named the marginal significance level, which the smallest significance level at which you can reject the null hypothesis.
Rejection rule with the p-value
- The rejection rule of rejecting the null is then the \(\text{p-value} < \alpha\).
Mathematically, the p-value is computed as
\begin{equation*} p\text{-value} = \begin{cases} \mathrm{Pr}_{H_0}\left(|z| > |z^{act}|\right)=2\Phi(-|z^{act}|) \text{ when } \sigma_Y \text{ is known} \\ \mathrm{Pr}_{H_0}\left(|t| > |t^{act}|\right)=2\Phi(-|t^{act}|) \text{ when } \sigma_Y \text{ is unknown} \end{cases} \end{equation*}
One-sided alternatives
- For a one-sided alternative hypothesis, \(H_1: \mathrm{E}(Y) > \mu_{Y,0}\), we can compute the p-value as \[ p\text{-value} = \mathrm{Pr}_{H_0}(t > t^{act}) = 1 - \Phi(t^{act}) \]
- The \(N(0, 1)\) critical value for a one-sided test with a 5% significance level is 1.64. The rejection region for this test is all values of the t-statistic exceeding 1.64.
Confidence Intervals for the Population Mean
Definitions
- A confidence set is the set of values that contains the true population mean \(\mu_Y\) with a certain prespecified probability.
- A confidence level is the prespecified probability that \(\mu_Y\) is contained in the confidence set. \(\text{confidence level} = 1 - \text{significance level}\).
- A confidence interval is the confidence set when it is an interval.
- In the case of a two-sided test for \(\mu_Y\), we say that a 95% confidence interval is an interval constructed so that it contains the true value of \(\mu_Y\) in 95% of all possible random samples.
Constructing a confidence interval based on the t statistic
- Step 1: we compute the t statistic for the two-sided test \[ t = \frac{\overline{Y} - \mu_{Y,0}}{SE(\overline{Y})} \xrightarrow{\text{ d }} N(0, 1) \]
- Step 2: we know that we fail to reject the null at the 5% level if \(|t| < 1.96\).
Step 3: we plug in the definition of \(t\) and solving for \(|t| \leq 1.96\), we get
\begin{align*} -1.96 & \leq \frac{\overline{Y} - \mu_{Y,0}}{SE(\overline{Y})} \leq 1.96 \\ \overline{Y} - 1.96 SE(\overline{Y}) & \leq \mu_{Y,0} \leq \overline{Y} + 1.96 SE(\overline{Y}) \end{align*}
The 95%, 90%, and 99% confidence interval
- The 95% confidence interval two-sided confidence interval for \(\mu_Y\) is \[ \{ \overline{Y} \pm 1.96 SE(\overline{Y}) \} \]
- 90% confidence interval for \(\mu_Y = \{ \overline{Y} \pm 1.64 SE(\overline{Y}) \}\)
- 99% confidence interval for \(\mu_Y = \{ \overline{Y} \pm 2.58 SE(\overline{Y}) \}\)
Comparing Means from Different Populations
Hypothesis tests for the difference between two means
- The question is whether there is a difference in earnings between male college graduates and female college graduates.
Let \(Y_{m, i}\) for \(i=1, \ldots, n_m\) be \(n_m\) i.i.d. samples from the population of earnings of male college graduate, i.e.,
\[ Y_{m,i} \sim IID(\mu_m, \sigma^2_m) \text{ for } i=1,\ldots,n_m \]
Let \(Y_{w, j}\) for \(j=1, \ldots, n_w\) be \(n_w\) i.i.d. samples from the population of earnings of female college graduate, i.e.,
\[ Y_{w,j} \sim IID(\mu_w, \sigma^2_w) \text{ for } j=1,\ldots,n_w \]
- Also, we assume that \(Y_{m,i}\) and \(Y_{w,j}\) are independent.
The null and alternative hypotheses
The hypothesis to be tested is whether the mean earnings for the male and female graduates differ by a certain amount, that is,
\[ H_0: \mu_m - \mu_w = d_0,\; \text{ vs. }\: H_1: \mu_m - \mu_w \neq d_0 \]
The test procedures: step 1
- Calculate the sample average earnings:
- \(\overline{Y}_m\) for the male and \(\overline{Y}_w\) for the female.
- As \(n_m\) and \(n_w\) get large, we know \(\overline{Y}_m \xrightarrow{\text{ d }} N(\mu_Y, \sigma^2_m/n_m)\), and \(\overline{Y}_w \xrightarrow{d} N(\mu_w, \sigma^2_w / n_w)\).
- Given that \(\overline{Y}_m - \overline{Y}_w\) is a linear function of \(\overline{Y}_m\) and \(\overline{Y}_w\), and \(Y_{m,i}\) and \(Y_{w,j}\) are independent, we know that \[(\overline{Y}_m - \overline{Y}_w) \xrightarrow{d} N(\mu_m - \mu_w,\; \frac{\sigma^2_m}{n_m} + \frac{\sigma^2_w}{n_w}) \]
Step 2
- When \(\sigma^2_m\) and \(\sigma^2_w\) are known, we use the z statistic \[ z = \frac{(\overline{Y}_m - \overline{Y}_w) - d_0}{\left( \frac{\sigma^2_m}{n_m} + \frac{\sigma^2_w}{n_w} \right)^{1/2}} \xrightarrow{\text{ d }} N(0, 1) \]
When \(\sigma^2_m\) and \(\sigma^2_w\) are unknown, we the t statistic \[ t = \frac{(\overline{Y}_m - \overline{Y}_w) - d_0}{SE(\overline{Y}_m - \overline{Y}_w)} \xrightarrow{d} N(0, 1) \] where
\begin{gather*} SE(\overline{Y}_m - \overline{Y}_w) = \left(\frac{s^2_m}{n_m} + \frac{s^2_w}{n_w} \right)^{1/2} \\ s^2_m = \frac{1}{n_m-1}\sum^{n_m}_{i=1}(Y_{m,i} - \overline{Y}_m)^2 \\ s^2_w = \frac{1}{n_w-1}\sum^{n_w}_{i=1}(Y_{w,i} - \overline{Y}_w)^2 \end{gather*}
Step 3
Calculate the p value: The p value for the two-sided test is calculated as
\[ p\text{-value} = 2\Phi(-|t|) \]
- For a two-sided test at the 5% significant level, we can reject the null hypothesis when the p value is less than 5%, or, equivalently, when \(|t| > 1.96\).
Confidence intervals for the difference between two means
- The 95% confidence interval can be constructed as usual based on the t statistic we have computed above.
The 95% confidence interval for \(d = \mu_m - \mu_w\) is
\[ (\overline{Y}_m - \overline{Y}_w) \pm 1.96SE(\overline{Y}_m - \overline{Y}_w) \]
Differences-of-Means Estimation of Causal Effects Using Experimental Data
- We define the outcome of a randomized controlled experiment to be \(Y\) and the binary treatment variable to be \(X\), \(X=1\) for the treatment group and \(X=0\) for the control group.
- Then the causal effect of the treatment can be conveniently expressed as the difference in the conditional expectation \[ E(Y \mid X=1) - E(Y \mid X=0) \]
Scatterplots, the Sample Covariance, and the Sample Correlation
Scatterplots
- Exploratory data analysis. Drawing graphs is an important aspect of exploratory data analysis to visualize the patterns of the variables of interests.
- A scatterplot is a plot of \(n\) observations on \(X_i\) and \(Y_i\), in which each observation is represented by the point \((X_i, Y_i)\)
An example of scatterplot
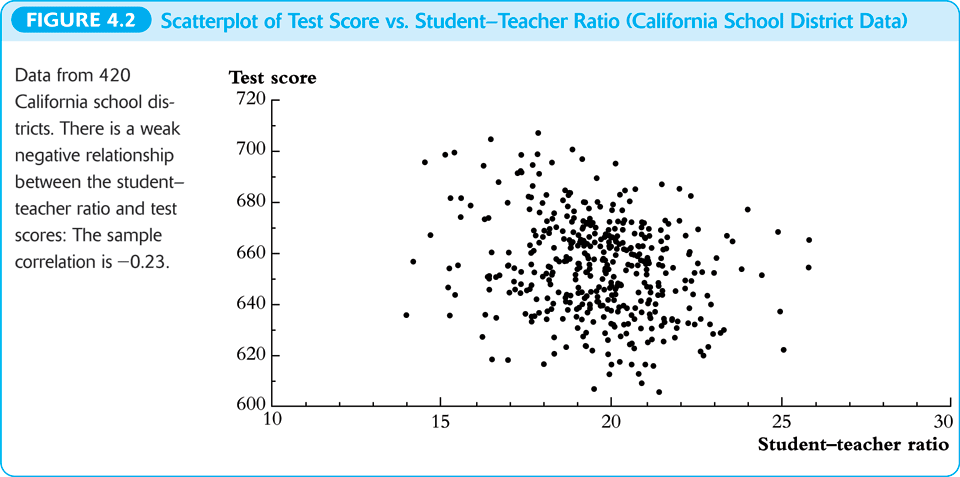
Figure 2: The scatterplot between test scores and student-teacher ratios
Sample covariance and sample correlation coefficient
- The sample covariance, denoted as \(s_{XY}\), is \[ s_{XY} = \frac{1}{n-1}\sum^n_{i=1}(X_i - \overline{X})(Y_i - \overline{Y}) \]
- The sample correlation coefficient, denoted as \(r_{XY}\), is \[ r_{XY} = \frac{s_{XY}}{s_X s_Y} \] and we have \(|r_{XY}| \leq 1\).
- If \((X_i,\, Y_i)\) are i.i.d. and \(X_i\) and \(Y_i\) have finite fourth moments, then \[ s_{XY} \xrightarrow{\text{ p }} \sigma_{XY} \text{ and } r_{XY} \xrightarrow{\text{ p } } \rho_{XY} \]
The correlation coefficient measures the linear association
We should emphasize that the correlation coefficient is a measure of linear association between \(X\) and \(Y\).

Figure 3: Scatterplots for four hypothetical data sets